缺陷孔洞识别
缺陷孔洞与非缺陷孔洞区别-借鉴思路
之前孔洞识别将所有封闭换都识别出来,但是存在的问题是,本身是封闭的正常部分也被识别,因此需要通过将两者区分开来;下图中都为所有孔洞,第三幅图中底部的圆孔为非缺陷孔洞,需要剔除。
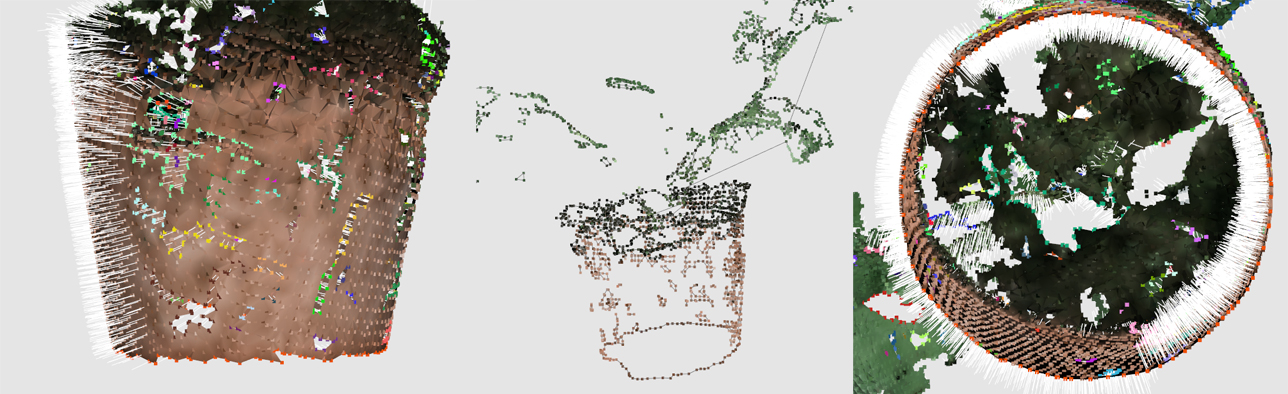
缺陷孔洞的检测方法思路
从孔洞的几何特性进行区分:
①周边表面不规则性;
②轮廓曲线不规则性;
步骤
1、通过曲率估计的方法对孔洞轮廓周边的点集进行聚类,表示方式有高斯曲率、平均曲率(这两者不一定适合),形状索引1,是范围(-1,+ I)中的数字,是尺度不变的。形状指数特别好地捕捉了“局部形状”的直观概念。形状指数可以映射到直观的自然色标。形状索引用于描述曲面上任意点在表面领域二极结构的一种方法:
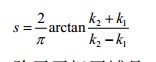
周边聚类的质心i的形状索引为:
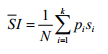
2、通过对轮廓曲线的曲率与扭力两个几何特性进行区分。通过测量轮廓的切向量变化来判断是否为缺陷孔洞;
文章里说缺陷孔洞的切线变化是杂乱无章的,非缺陷孔洞在切线角度上的变化是平滑过渡的。
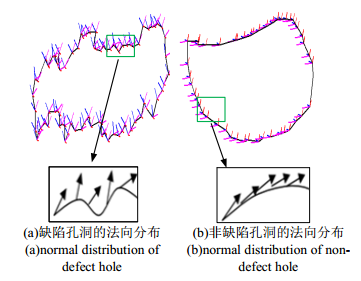
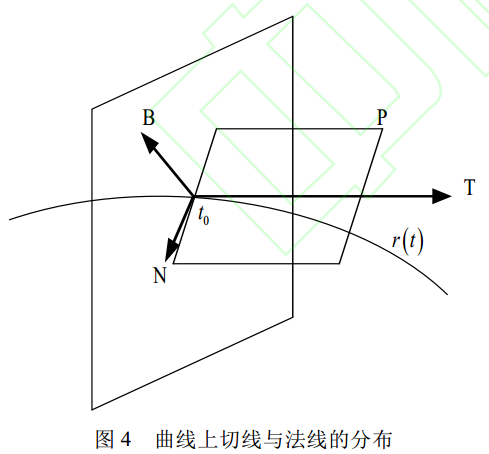
实际情况
植株的实际情况不同:

小型孔洞(多为缺陷孔洞,如上图-右)个点法向量较为一致,差异较小;
大型孔洞(如上图-中)法向量部分超圆内,部分朝圆外,差异较大;
按照上述思路,通过法向量差异进行判断,那么法向量差异小的为缺陷孔洞,法向量差异大的为非缺陷孔洞;
思路:依次获取孔洞个点的法向量,并比较向量两点法向量的角度差,即每条边两个顶点的角度差,计算平均角度差与标准角度偏差,小于设定阈值为缺陷孔洞,否则不为缺陷孔洞
伪码:
1 | vector<vector<vertex>>holes_out; |
结果
设定平均角度阈值为0.4(22.9°),rmse阈值为0.5
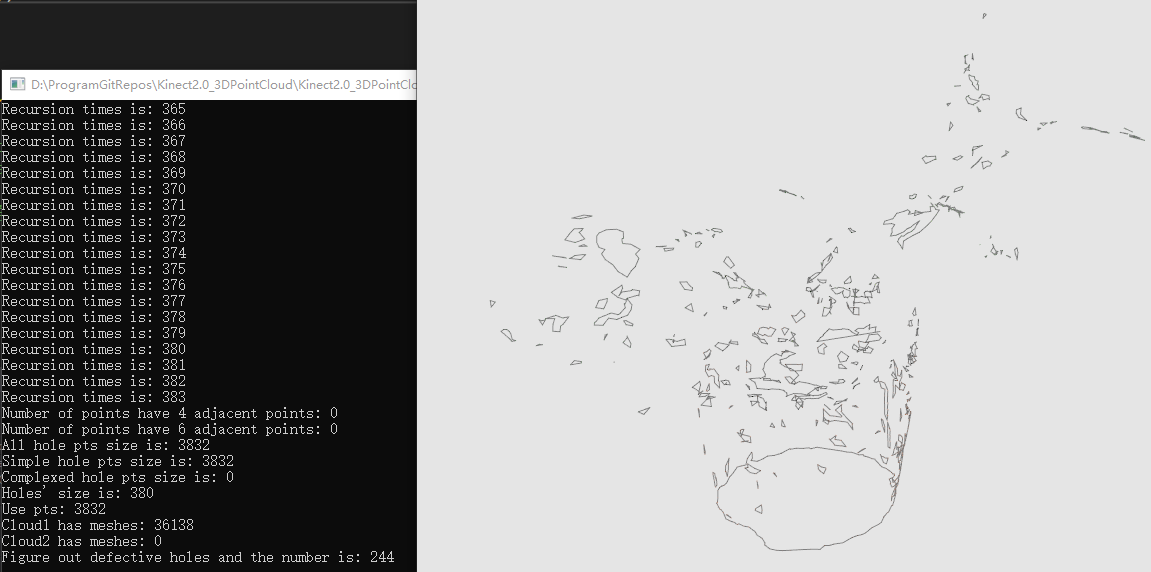
设定平均角度阈值为0.2(11.45°),rmse阈值为0.5
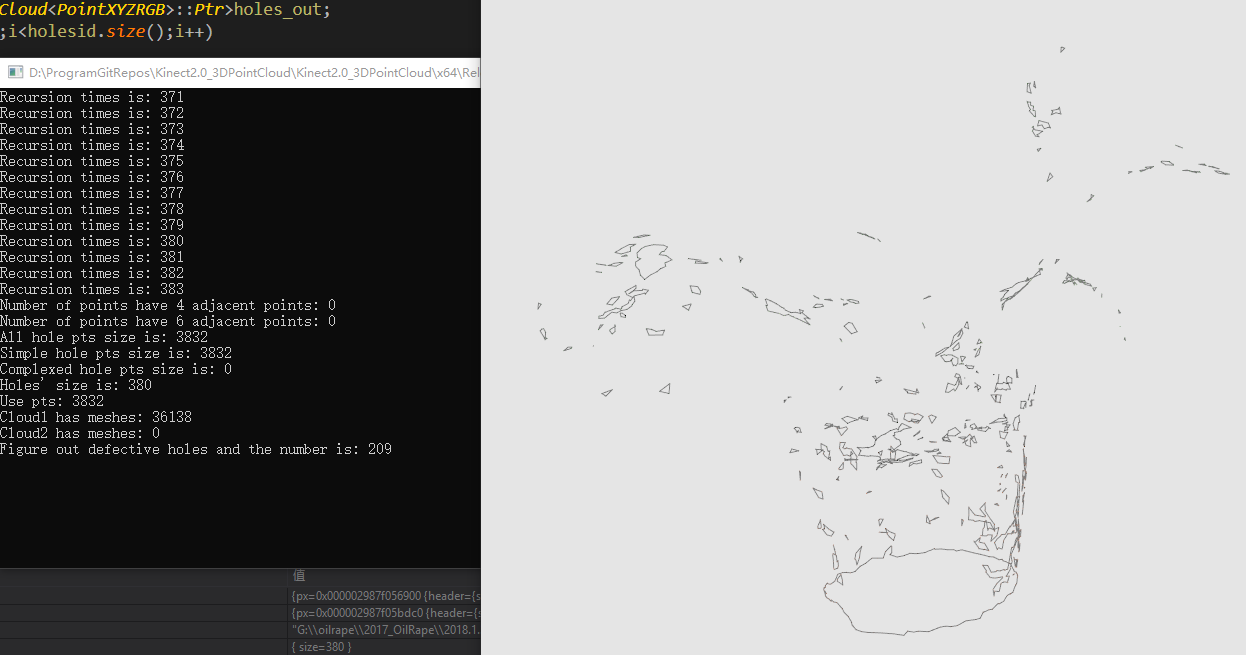
设定平均角度阈值为0.4(22.9°),rmse阈值为0.3
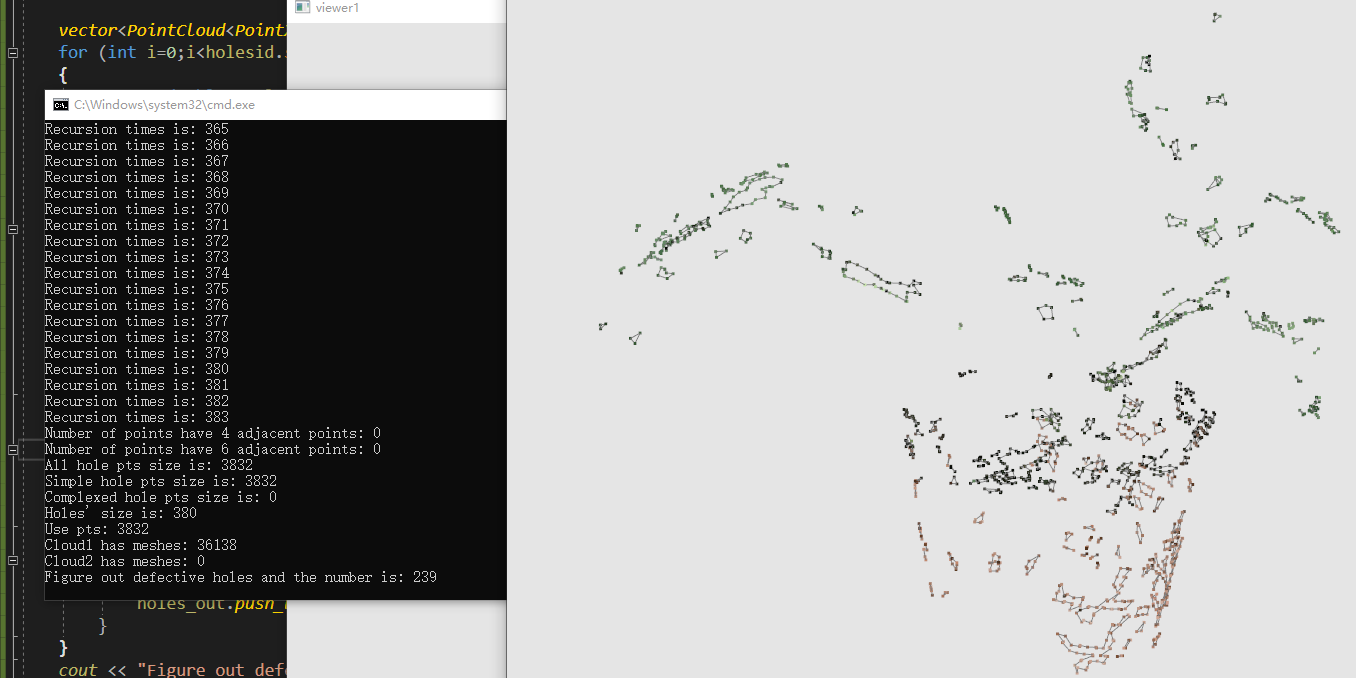
设定平均角度阈值为0.6(33.4°),rmse阈值为0.3
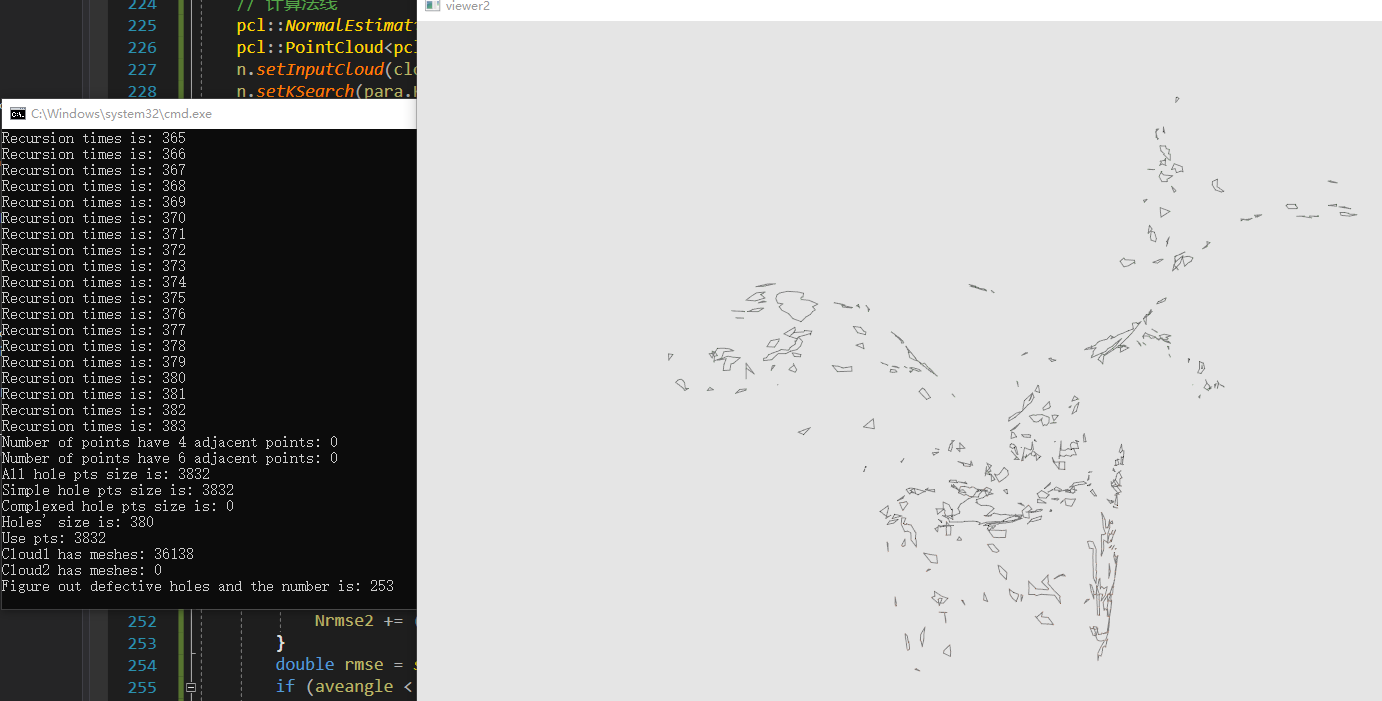
设定平均角度阈值为0.6(33.4°),rmse阈值为0.1

设定平均角度阈值为0.4(22.9°),rmse阈值为0.3
因此,平均角度阈值与rmse阈值对于孔洞有一定效果
但是仍存在一些问题:不封闭孔洞,以及半边数据构成的孔洞实际为单独的面片结构。
相关引申资料概念
平均形状概念
基于形状索引特征的平均值
形状索引特征概念
一种特征描述子,与形状相关,可有曲率、法向量等信息表示;
图形特征
对象识别特征
1、对于类间变化敏感,有效区分对象与背景;
2、类内不变形,对同一个对象在不同的角度、光照、表情(人体)、弯曲情况(植株叶片)的变化具有一定的不不变性。手工特征:Gabor,LBP,SIFT;无监督学习:LE;
导数表
