主要提取的点云特征:
一、主曲率
点在平面的移动速度,陡峭程度;
计算方式:
Step1:pj(px, py, pz)点的法向量nj(nx, ny, nz)投影到法向量ni(nix, niy, niz)和点pi(pix, piy, piz)构成的切平面,pj是pi的领域点:
切平面表示:nix (x-pix) + niy (y-piy) + niz (z-piz)=0;
各点法向量投影表示: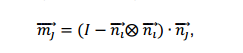
其中,I是3×3的单位矩阵;
注:向量 $\vec{n_i} \bigotimes \vec{n_i}$表示两法向量直积,但是个人认为这里应该是发现了的列向量直积列向量转置,否则无法得到3×3的单位矩阵,最后得到矩阵a应该是:
a = \left[
\matrix{
1-nix·nix & nix·niy & nix·niz \
niy·nix & 1-niy·niy & niy·niz \
niz·nix & niz·niy & 1-niz·niz \
}
\right]
\matrix{
(1-nix·nix)·nx+nix·niy·ny+nix·niz·nz,\
niy·nix·nx+(1-niy·niy)·ny+niy·niz·nz,\
niz·nix·nz+niz·niy·ny+(1-niz·niz)·nz, \
}
$$
然后计算协方差的特征向量得到三个λ,则通过大小排序可得到最大与最小曲率以及曲率方向
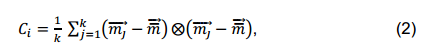
二、半径表面特征
得到设定半径内,领域点与计算点的法线夹角与亮点距离,这两个统一作为一个特征;
三、PFH点特征直方图
加快的还有FPFH
四、SHOT 方向直方图特征
Signature of histogram of orientations
构造方法:以查询点p为中心构造半径为r 的球形区域,沿径向、方位、俯仰3个方向划分网格,其中径向2次,方位8次(为简便图中径向只划分了4个),俯仰2次划分网格,将球形区域划分成32个空间区域。在每个空间区域计算计算落入该区域点的法线nv和中心点p法线np之间的夹角余弦cosθ=nv·np,再根据计算的余弦值对落入每一个空间区域的点数进行直方图统计,对计算结果进行归一化,使得对点云密度具有鲁棒性,得到一个352维特征。(原论文:Unique Signatures of Histograms for Local Surface)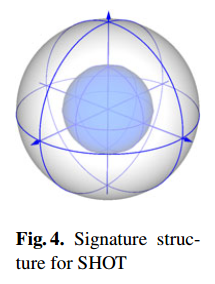
五、Spin image旋转图像
https://blog.csdn.net/renyuanxingxing/article/details/83279328
三维点云深度学习分类

PointNet&PointNet++
PointNet的问题
PointNet对每个点表征,未考虑点邻域信息,局部信息描述不足;maxpooling最后提取的是全局特征,损失较多信息;分割网络是将点特征与全局特征拼接,描述能力有限。
PointNet++中用到了FPS最远点降采样,相比随机降采样的优势:尽肯能广泛考虑覆盖空间中的所有点(包括噪声)
Point++中的Group layer寻找领域点是在坐标空间进行,采用的是KNN或者query ball point,并没有考虑特征空间的相似性。
Query ball更加适合于应用在局部/细节识别的应用上,比如局部分割。
PointNet++和PointNet的区别在于:
类比CNN,pointnet可以看做一个卷积层,因为他通过max pooling后考虑的是整个点集的全局特征。若果这个点集是全体点集的一部分,那么可以发现PointNet与CNN的卷积核类似。而PN++则是在此基础上考虑了局部的信息,并对分层局部特征进行了整合。
其中,在Point Layer层,主要分为了三个步骤
1)point feature embedding
2)pooling in local regions
3)further processing
其中,步骤1是进行特征维度调整,将多维特征(x,y,z,nx,ny,nz, 其中n为法向量)等通过1×1的卷积核进行线性组合实现升维或者降维,从而达到嵌套的目的;步骤2是以某点P为中心,将邻域点的特征信息进行整合来描述该点P的局部特征,这里用的是pooling(可以是,max,mean等)。继续做1×1的卷积,这个步骤论文没有用,实际上也没有必要,因为这个时候的数据就是最远点采样后的点及特征,继续将这些采用点整合的话,又变成一个全局性的,尺度在此变大。当然考虑到多个尺度的可以卷积,但是1×1的卷积如果不非线性变化的话没有太大的意义。
点云深度学习借用的先验知识有限;